Home About Les Staves In-House Training Publications Articles Numeracy Framework P Scales Downloads Contact

Magnifying Maths Mathematics for children with profound and complex learning difficulties Reaching the parts of Mathematics that the National Curriculum does not reach Contents Summary The parts of Maths which the National Curriculum does not reach Personal and Social Mathematics − the basis for a relevant curriculum Tools and processes of learning Tools for Early Learning Processes That Use The Skills Content of the Learning Experience The Tool Box Perceptual Skills Sensorimotor Development − Exploratory Skills Communication and Thinking Looking Deeply into Programmes of Study The value of the view from above References Summary Expanding on the idea of "Personal and Social Mathematics" which was introduced in the article "Rhythm of Life". This article looks at mathematics and how it connects to many important areas of learning for children with profound and complex learning difficulties, and how all that relates to the National Curriculum. The parts of Maths which the National Curriculum does not reach Of all the National Curriculum subjects Mathematics causes teachers of children with profound learning difficulties a special level of concern. In part this is due to the general conception of mathematics as an academic subject involving symbolic representations and computation. This misconception is discussed in my previous article, which set out to illustrate that concepts of space, time, and quantity permeate our lives, and that these aspects of mathematics are essential to our daily functioning and enjoyment. However it cannot be denied that the National Curriculum Programmes of Study reinforce the misconception. The earliest "Statements of Attainment" assume that even before they start school children have mastered ideas and skills that pupils with profound barriers to learning will in fact pursue for the rest of their lives. The programmes of study do not give any guidance about the teaching of concepts that underlie understanding about changing quantities, space and time. In this respect they fail to support pupils entitlement because they do not include material that will enable pupils with severe learning difficulties to progress and demonstrate achievement. To do this it is necessary to enhance the Programmes of Study to provide an outline for teaching that reaches the parts of Mathematics which the National curriculum does not reach. Figure 1: Personal and Social Mathematics Personal and Social Mathematics - the basis for a relevant curriculum "Personal and Social Mathematics" was described in my previous article "Rhythm of Life" and is summarised in Figure 1. It encompasses the earliest stages of learning mathematics for all children. These activities are the basis for the development of broad understandings that lead to mathematical concepts, and readiness for numeracy. Children with severe barriers to learning may be exploring these stages of mathematical development throughout their school lives. 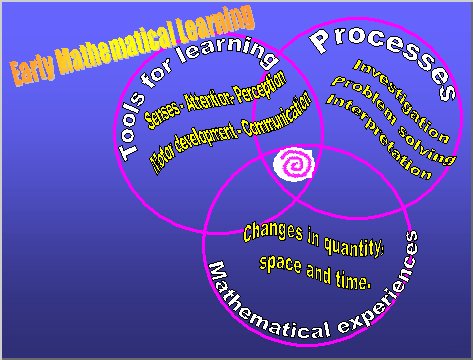Tools and processes of learning The processes that children use gathering and understanding information are not confined to mathematics. It is however useful for us to consider them to understand how "Personal and Social Mathematics" begins to evolve. Likewise though the regular processes of development are disrupted by the complexity of disabilities children suffer, an awareness of the usual course of learning provides guidance for planning special teaching strategies. There are a number of strands important in early learning. Each of the strands is itself composed of a number of threads, none of these processes takes place alone. To understand how learning happens it helps if we unravel the braid. The first important strand might be described as -- Tools for Early Learning -- but as they are used the tools are also refined, using them is itself part of a process of development. Threads within this strand include :- Sensory and motor development Attention skills Perceptual skills These are skills used to collect and process information. there are obvious barriers that make it difficult for children with learning difficulties to acquire them. During the seventies when schools for pupils with severe learning difficulties were first searching for an identity and a curriculum, there was a tendency to concentrate on teaching skills in isolation. A shortcoming of this approach was that it did not acknowledge that children's learning is rarely detached from other experiences. Children also learn as they use their skills to explore, and in that process are stimulated to relate their knowledge to the wider environment. As children collect information using these skills, are naturally encouraged to use communication skills, both to express and seek information, all of these processes together contribute to the development of ideas and concepts. So there is a second important strand of -- Processes That Use The Skills -- they give life and breadth to the curriculum by drawing in content from the real world and encouraging the positive activity of exploration. Such processes both stimulate and use learning. The threads in this strand are:- Investigation − exploration, stimulus response, discriminating, associating connecting and chaining. Concept learning. Problem solving − Combining concepts, using them together, realising rules, anticipating results. Interpretation − Using rules applying them to other situations, transfer of learning. Generalising connecting / creating new combinations. As children use these processes they gather experience, and generate further opportunities to experience and act upon the environment. The third strand is the -- Content of the Learning Experience. When the "skills and processes" are brought to bear on subject content, in this case mathematical experiences, they promote the development of related concepts and abilities, the relationship is illustrated in figure 2. Devising an appropriate curriculum and learning activities involves considering the associations between: Skills which pupils need to learn and use. Processes in which children need to involve themselves in order to learn. Appropriate content for investigations − in this case mathematical experiences. Such consideration may help us to enhance the existing Programmes of Study by giving us ideas for more detailed activities which are relevant to pupils with profound learning difficulties. Figure 2: Components of early mathematical learning The Tool Box To create some idea about how we should substantiate the programmes of study it will be useful to take a look at the tools and processes of learning, and some of the ways that barriers to learning affect our pupils use of them. Figure 3: Sense Attention and Perception Perceptual Skills Perception is a complex process, filtering, attending to and interpreting sensory information in what seems an instant. Its component processes work together. Some of the features that we might wish to consider teaching are illustrated in figure 3. It is important to remember that we depend upon our previous knowledge to give us structures into which we fit new information and shape our perceptions. As Kant remarked -- "We see things not as they are, but as we are" Shortcomings in existing ideas will confuse perceptions, this has obvious implications for children with sensory impairments. For example, the environment has less stimulus value for visually impaired children and they are restricted in their engagement within it. They may not recognise their impact on objects they manipulate; will not experience the same visual models, nor have the same fund of visual memories to match against stimuli, (Hendrickson and McLinden 1977). Paradoxically a classroom environment can be too busy, with extraneous noise, or a light room have too many effects competing for attention, to promote focus. Hearing impaired children will not experience sounds associated with objects or events, which draw attention and support connections. Neither will they have recourse to instruction or description in the form of spoken language. These examples highlight the importance of how we present sensory stimulation to pupils and the need to offer alternative channels, to focus attention and facilitate interpretation. The evolution of the "Sensory Curriculum", (Longhorn 1988) has provided many avenues for developing alternative channels. Innovative work has also conceived well organised environments that make stimulation accessible, e.g. Lilli Nielsen's little room and resonance boards, (1987) and enable focus of attention e.g. Keith Park's use of tents (1997). It is essential that these attitudes and techniques permeate the presentation of the mathematics curriculum for sensory impaired children, since one of their primary needs is to engage in exploration which helps them develop understanding of form, and changes as they affect their environment. Figure 4: Some Early Stage of Exploration Sensorimotor Development − Exploratory Skills By five months a child can intercept a moving object. By nine months adjust the width and orientation of their grasp to match the size and shape of objects they intend to pick up. − Some complex practical mathematical calculations have been taking place. As children become able to co-ordinate the interaction of their sensory and physical abilities, there is more than physical development at stake. They reach out to the world for stimulation and lay down important foundations of information gathering. From these beginnings wider skills develop, stimulating communication and awareness that things still exist even when out of sight. This simple notion heralds the beginning of reasoning and abstract thought. Some phases of this journey, driven by curiosity, are described in figure 4. Children with physical, sensory, or cognitive disabilities will be disadvantaged in this realm of learning. They will require strategies, including alternative channels to help them explore it. Many physical activities of the sensorimotor period can be seen to relate directly to mathematical concepts, e.g. holding a balloon with both hands has obvious connections to experience of space, shape etc. However other implications are more subtle, e.g. a driving force of learning is cerebral patterning generated by primary and secondary circular movements − thus the exploration of space itself has a role in cerebral development. The effects of shortcomings in such processes are acknowledged in descriptions of specific learning difficulties such as dyspraxia. Considering the effect of sensory and physical barriers to learning, they must also be part of the complexity of learning difficulties endured by very special pupils. There is reason therefore for including sensorimotor activities that not only include exploration of size, shape, weight etc. but also manipulation, movement, and focus of attention, as part of the mathematics curriculum for very special children. Communication and Thinking Concepts It is hard for us to imagine concepts without symbolic verbal description because we are linguistic beings. We may use directive speech under our breath when under pressure. Or use egocentric speech aloud in private to rehearse our thoughts about an emotional or stressful event. We may if required be able to describe some of our conceptual understandings using words, but for the most part we perceive our world, and control our activities without recourse to using linguistic thinking, our internal activities are speechless. This is not to say lacking in profundity. Einstein described his mathematical thinking as "Initially involving visual and muscular processes" only later being turned into words and symbols. Most children with complex learning difficulties have either no language or severely disrupted language. However the child who can intercept a moving object has a practical concept of "vectors", related concepts are essential at many levels; to feed yourself, control a wheelchair; or cross a road. This and many other examples illustrate that non-verbal, non-symbolic, forms of mathematical concepts are relevant to children, long before their language has developed enough to enable them to use reason to describe and organise intellectual structures. 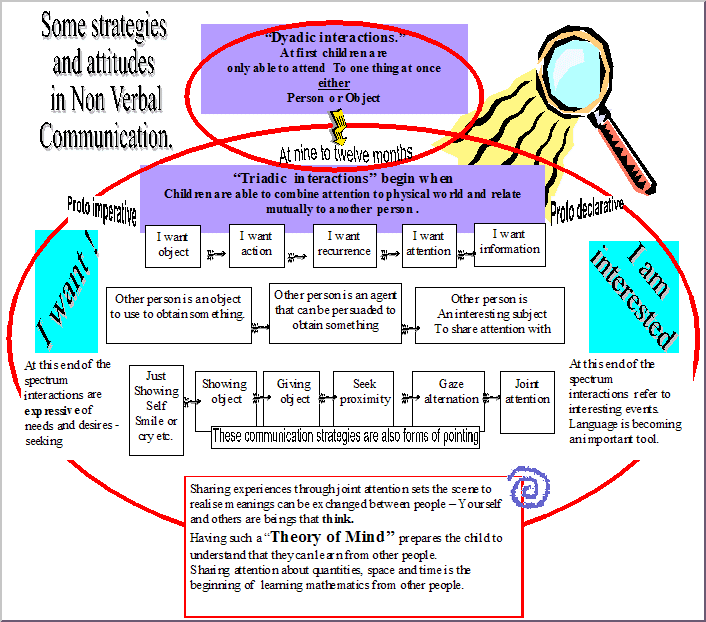Figure 5: strategies and attitudes found in non-verbal communication Communication Strategies We need to communicate with our pupils about mathematical experiences. The features of strategies and attitudes found in non-verbal communication, as illustrated in Figure 5, may show us the kinds of response we can expect when working with pupils whose communication is at early levels. Their responses may be impeded by physical or sensory difficulties and our role is to help them overcome constraints. Some of the ways we might do this would be to, teach alternative pointing skills; and non verbal conversation strategies, use augmented communication and signing; facilitated communication; and objects of reference. We should always seek to match and advance their stages and apply these strategies in age appropriate ways. Expectations Working with non-verbal pupils requires that we seek to understand their reactions, and elicit appropriate responses from them, whilst we use language and alternative communications that illustrate and support the content of our teaching. A noteworthy problem arises here. A process of sensing where the child is at and pitching input a little higher usually stimulates the progression of language that adults' use with children. There is evidence of a negative spiral when children do not advance the nature of their responses, (Rondal.J.A. 1977). Adults revert to using language with more closed questions and commands, controlling and instructing rather than using "referential" terms that describe or explore events. The exploratory nature of the adult child discourse is therefore reduced, (Nelson, K, 1973). A situation we need to rectify. Awareness of self and others The learning and progress pupils make through their interactions is about more than "communication" it is about personal development. We have seen that there is parallel progression from self-centered investigation, to social interaction in the development of communication and sensorimotor skills. In effect, both aspects of learning enable children to be more social and more curious. They also encourage the child's progress towards greater awareness of themselves and others. Having a "Theory of Mind" i.e. realising that they, and others are creatures which think, enables them to understand other people and the world around them, (Dunn 1988). It enables them to realise that other people "know" and they can learn from them. It is an essential at the core of learning, that we need to cultivate. A special role for mathematics Mathematics has a special part to play in that core of learning, a part which has two dimensions:- Its content describes the facts and realities of the physical world, providing essential information we need to construct our concepts. The facts and realities of the real world provide a medium of interest for us to observe and share. Joint attention to the nature of objects and events encourages adults to sustain a "referential" language input, and therefore encourages curiosity and exploration. It provides opportunities to develop communication skills and stimulates the development of the child's "theory of mind." Whilst these are clearly aspects of personal and social development there is also a wider "human" aspect, a spiritual dimension, in that it brings about a consciousness of: "I am the one. − We are together." Communication about mathematical events can be seen to promote learning that crosses developmental and curriculum boundaries. A recent report in the Times Educational Supplement (TES) "Numbers help with words", cites evidence that in some schools pupils participating in numeracy groups showed related improvements in English. The world is rich in events relating to personal and social mathematical development. Looking closely to see how these events relate to our children's needs and abilities we can find ways to meet the challenge of enhancing the National Curriculum, so that it reaches the parts of mathematics which are important to our pupils. Looking Deeply into Programmes of Study By taking a magnifying glass to the National Curriculum descriptions of learning opportunities, we will find within them experiences that could be beneficial for pupils with severe or complex learning difficulties. For example Math's Attainment Target 1 at Key Stage 1 states that pupils should :- Use and apply mathematics in practical tasks, in real life problems and within mathematics itself. Explain their thinking to support the development of their reasoning. To extend the statements to relate to material which is relevant to our pupils abilities, and provide detail about aspects of the learning necessary to work towards the described attainments. We might enhance them in this way:- To include − Experience and relate to changes in objects / materials / space and time Make things change. Control the nature of change. To include − Respond to changes Communicate about the effects of changes. Communicate about how they expect or would like things to change. These enhancements underpin the other teaching points in A.T.1 Such enhancements are a starting point In turn they can be interpreted into a variety of more specific practical activities, suitable for individual pupils, and inclusion into a variety contexts. T hey can be appropriate to specific math's lessons, other subjects, thematic teaching, or everyday activities. A few of many possible ways of providing practical experiences which match the above criteria are:- Knocking skittles over in variety of ways: − with a ball on a string suspended from the ceiling, or running them down in your wheel chair − this could be part of a specific math's lesson involving, -- anticipating change, making things change, responding to change, experiencing the concept of "more" hearing counting related to events, enjoying mathematical events etc. Anticipating music, or controlling sound or light − making things change, with switches might occur in cross curricular circumstances − Music or Science. Communicating about choices or quantities of food or that their cup is now empty may occur at dinner time. The processes of investigation, problem solving, and interpretation / generalisation occur in all these circumstances. The same approach can be taken with other attainment targets. (A future article will give more detail relating to the processes of counting in A.T.2). In all the activities, we should remember the emphasis we have placed on "joint attention" and sharing descriptions, the adult plays an important role eliciting, sharing, reinforcing, extending, and connecting responses. Each of the activities can provide a variety of levels of experience and attainment, a useful aid to recording pupils very early levels of response has been described by Erica Brown using the categories:- Encounter Awareness Response Engagement Participation Involvement Achievement Since the first publication of this article these categories have become the basis of the P Levels that are now generally used as tools of assessment and to show pupils of very special pupils. More information can be found by following this link and downloading the handout called "P Levels and the National Numeracy Strategy". The value of the view from above The model of enhancement that I have used takes a "top down" view, looking down into the National Curriculum for underlying learning. When we consider learning at these fundamental levels we are often tempted to think in terms of "bottom up" approaches, starting with basic skills and listing a ladder of ability levels which climb towards access to the first rungs of the National Curriculum. Some people may see the P Levels in this way -- we should remind ourselves that the QCA guidelines 2001 emphasise the importance of lateral development. There is value in having clear ideas about developmental steps but there is also value in taking an overview,like looking through a microscope it reveals the microcosm of activity which underlies apparently small steps of learning. Such an overview will often illustrate the breadth of learning that is needed at each level and it often exposes the connections mathematics makes with other areas of learning and personal development. Appreciation of this complexity illustrates to us the value of achievements made when children with complex learning difficulties learn to appreciate themselves, other people, and the world around them. Such appreciation provides a strength to those who choose to face the difficult task of unraveling and teaching the minutiae of individual learning. It may help them if they see the value and complexity of their work acknowledged. "Seeing the world in a grain of sand, and heaven in a wild flower. Holding infinity in the palm of your hand, and eternity in an hour" William Blake References "Planning the curriculum for pupils with Profound and multiple learning difficulties" SCAA publications London (1996) Hendrickson, H. Mclinden, M. (1977) Implications of a visual impairment for early communication development. The SLD Experience. Issue 17. Kidderminster. Longhorn, F .(1988) A Sensory Curriculum for Very Special People. Souvenir Press. Nielsen, L. (1987) Spatial Relations in congenitally blind infant. Kalundbork, Denmark: Refnarskolen. Park, K. (1997) Loitering within tent. SLD Experience Issue 18 Kidderminster. Rondal, J.A. (1977) Maternal speech to normal and Downs syndrome children. In Mittler.P. Research int practice in mental retardation education and training. Vol. 2. Baltimore Y.P.P. Nelson, K. (1973) Structure and strategy in learning to talk. Society for research into child development Monograph 149. No.s 1-2 Yale. University. Dunn, J. (1988) The beginnings of social understanding. Oxford. Blackwell. Times Educational Supplement 26.2.99 Page 7. Brown, E. (1996) Religious Education For All. London. David Fulton. Access − Mathematics. Equals (1997.) University of Northumbria. Baseline Assessment and curriculum target setting for access to the National Curriculum. (1998) Equals Tyne & Wear. This article by Les Staves was first published in Issue 117 of Special Children under the title "Painting By Numbers". Les Staves Retired as the head teacher of Turnshaws Special School in Kirklees following an outstanding Ofsted report. He has thirty years teaching experience in mainstream and special education. He now works as a freelance trainer and consultant.